在Vue2中,采用了双端diff算法.而Vue3借鉴并拓展了快速diff算法.快速diff的实测速度非常快,这一章我们着重讨论快速diff的实现原理.
# 预处理
不同于简单diff和双端diff,快速diff包含预处理步骤,处理相同的前缀和后缀节点.
假设两组子节点的顺序如下:
- 旧: p-1 p-2 p-3
- 新: p-1 p-4 p-2 p-3
我们可以发想两组子节点有相同的前置节点p-1和相同的后置节点p-3,p-4.
对于相同的前后置节点,我们无需改变它的位置,只需要打布补丁即可.
对于前置节点,我们可以建立索引j,起初始值为0,用来指向两组节点的开头,开启一个while循环,让j递增,直到遇到不相同的节点为止.
function patchkeyedChildren(n1, n2, container) {
const newChildren = n2.children
const oldChildren = n1.children
//处理相同前置节点
let j = 0
let oldVNode = oldChildren[j]
let newVNode = newChildren[j]
//循环遍历
while (oldVNode.key === newVNode.key) {
patch(oldVNode, newVNode, container)
j++
oldVNode = oldChildren[j]
newVNode = newChildren[j]
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
接下来我们要处理相同的后置节点.由于两组子节点长度可能不同,我们需要两个索引分别指向新旧两组子节点的末尾.
function patchkeyedChildren(n1, n2, container) {
const newChildren = n2.children
const oldChildren = n1.children
let oldEnd = oldChildren.length - 1
let newEnd = newChildren.length - 1
let oldVNode = oldChildren[oldEnd]
let newVNode = newChildren[newEnd]
while (oldVNode.key === newVNode.key) {
patch(oldVNode, newVNode, container)
oldEnd--
newEnd--
oldVNode = oldChildren[oldEnd]
newVNode = newChildren[newEnd]
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
这一步操作之后,两组子节点的状态如下:
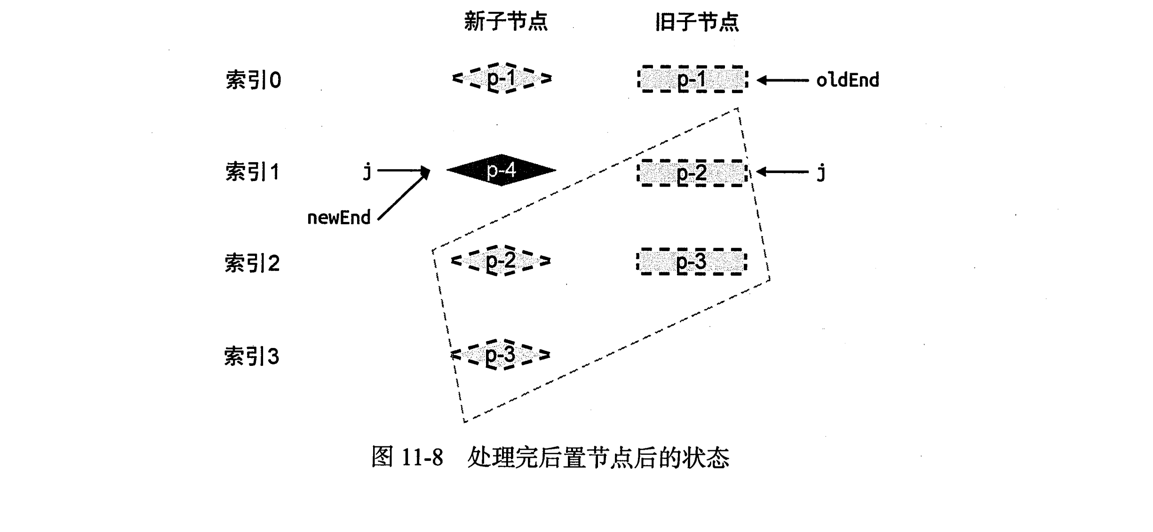
由图可知,旧的一组子节点已经被全部处理了,而在新节点中还遗留一个未处理节点p-4.不难发现,p-4节点是一个新增节点.
我们需要用程序得出"p-4是新增节点",这需要我们观察索引之间的关系.
- oldEnd < j 成立:说明在预处理中,所有的旧节点被处理完了
- newEnd >= j 成立: 说明预处理之后,新节点中还有剩余节点没有处理,这些节点都是新增节点,我们需要把他们挂载到正确的位置上.
在新的一组子节点中,j和newEnd之间,都需要作为新增节点进行挂载.我们需要找到正确的锚点元素.
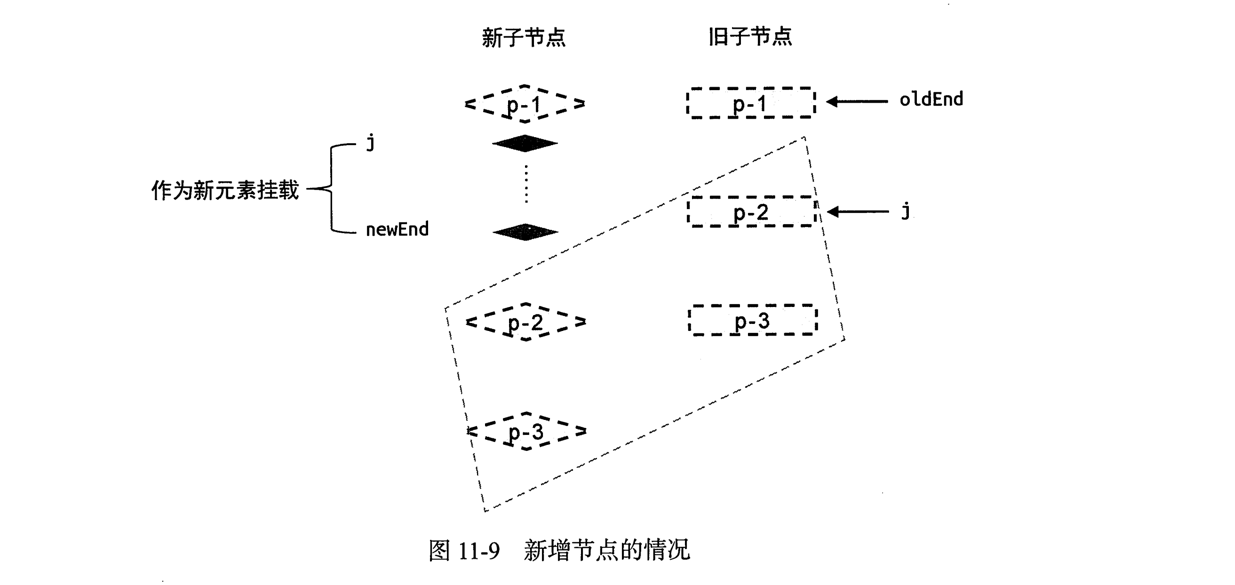
观察图可以知道,节点p-2所对应的真实dom节点就是挂载操作的锚点元素.
function patchkeyedChildren(n1, n2, container) {
const newChildren = n2.children
const oldChildren = n1.children
//预处理完成后,如果满足如下条件,进行新节点的挂载
if(j > oldEnd && j <= newEnd) {
//锚点的索引
const anchorIndex = newEnd + 1
//锚点元素
const anchor = anchorIndex < newChildren.length ? newChildren[anchorIndex].el : null
//while循环挂载
while(j <= newEnd) {
patch(null, newChildren[j++], container, anchor)
}
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
同样的,我们可以联想到删除节点的情况,预处理以后如图:
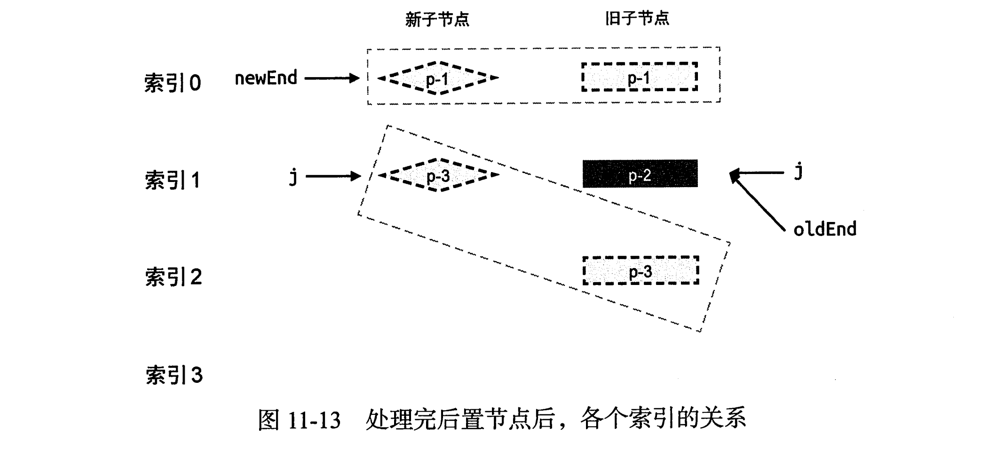
当预处理完成之后,在旧节点中遗留了一个节点p-2,毫无疑问,我们应该卸载p-2,实际上,遗留的节点可能有多个.
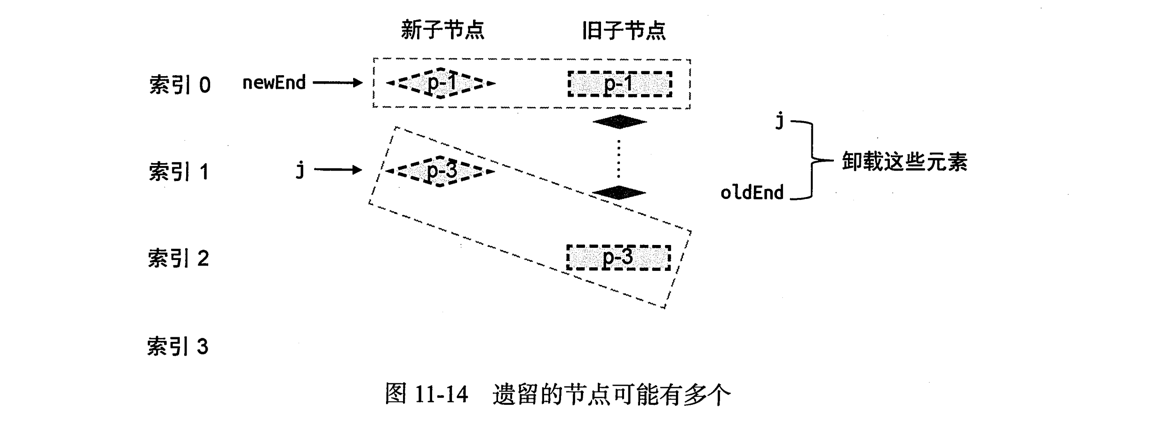
索引j和索引oldEnd之间的任何节点都应该被卸载.
function patchkeyedChildren(n1, n2, container) {
const newChildren = n2.children
const oldChildren = n1.children
//省略预处理
if(j > oldEnd && j <= newEnd) {
//挂载
} else if(j > newEnd && j <= oldEnd) {
// 卸载
while(j <= oldEnd) {
unmount(oldChildren[j++])
}
}
}
2
3
4
5
6
7
8
9
10
11
12
13
# 判断对节点是否进行移动操作
之前的节点过于理想化,预处理之后,总有一组子节点处理完毕.在这种情况下,我们不需要进入到快速diff的核心部分,只需要简单的挂载和卸载即可.但情况总不会这么理想.
假设两组子节点如下:
- 旧: p-1 p-2 p-3 p-4 p-6 p-5
- 新: p-1 p-3 p-4 p-2 p-7 p-5
在这个例子中,预处理只能处理前后两个节点,现在,新旧节点都有部分节点未处理.
diff算法的核心在于:
- 判断是否有节点需要移动,以及该如何移动
- 找出新增和被移除的节点
在这种非理想情况下,我们需要新增一个else分支处理.
# 核心思路
我们需要构建一个数组source,长度等于新子节点组在经过预处理后的长度,每个元素初始值为-1,如图:
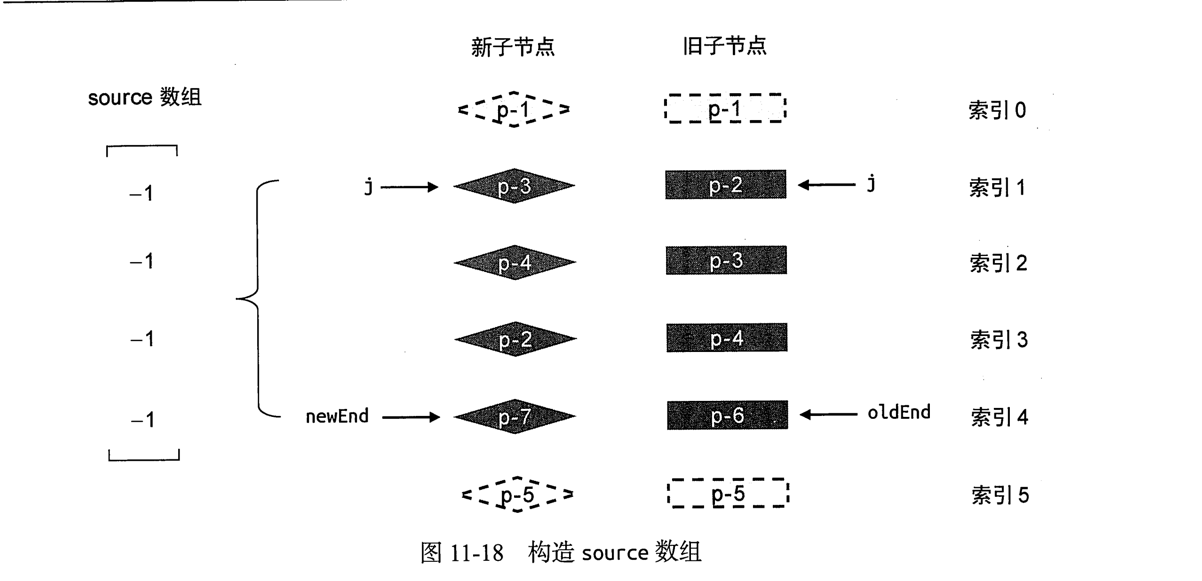
通过一下代码完成数组构造
const count = newEnd - j + 1
const source = new Array(count)
source.fill(-1)
2
3
我们会使用source数组来存储新子节点组中节点在旧子节点组中的位置索引,后续使用它计算出最长递增子序列,用于辅助完成DOM移动的操作.
我们可以使用索引表来快速填充source数组(hashMap),实现代码如下:
count = newEnd - j + 1
const source = new Array(count)
source.fill(-1)
const oldStart = j
const newStart = j
const keyIndedx = {}
for(let i = newStart; i <= newEnd; i++) {
keyIndedx[newChildren[i].key] = i
}
//遍历旧子节点组寻找未处理节点
for(let i = oldStart; i <= oldEnd; i++) {
const oldVNode = oldChildren[i]
//找到新子节点组中具有相同key的节点索引
const k = keyIndedx[oldVNode.key]
if (typeof key !== 'undefined') {
newVnode = newChildren[k]
patch(oldVNode, newVnode, container)
//填充数组
source[k - newStart] = i
} else {
//没找到就该卸载
unmount(oldVNode)
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
接下来我们需要判断节点是否移动.有点类似于简单diff算法.
const count = newEnd - j + 1
const source = new Array(count)
source.fill(-1)
const oldStart = j
const newStart = j
let moved = false
let pos = 0
const keyIndedx = {}
for(let i = newStart; i <= newEnd; i++) {
keyIndedx[newChildren[i].key] = i
}
for(let i = oldStart; i <= oldEnd; i++) {
const oldVNode = oldChildren[i]
const k = keyIndedx[oldVNode.key]
if (typeof k !== 'undefined') {
newVnode = newChildren[k]
patch(oldVNode, newVnode, container)
source[k - newStart] = i
//判断节点是否需要移动
if (k < pos) {
moved = true
} else {
pos = k
}
} else {
unmount(oldVNode)
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
我们新增了两个变量moved和pos,前者初始值为false,代表是否需要移动节点.后者存储着遍历旧节点组 过程中 遇到的最大索引k.如果遍历过程中遇到的索引值都是递增趋势,则说明不需要移动节点.所以我们在第二个for循环中比较j和pos来判断是否要移动节点.
除此之外,我们还需要一个数量标识,代表已更新过的节点数量,已更新过的节点数量应当小于新子节点中需要更新的数量.
let patched = 0
if(patched < count) {
if(typeof k !== 'undefined') {
newVnode = newChildren[k]
patch(oldVNode, newVnode, container)
patched++
}
} else {
unmount(oldVNode)
}
2
3
4
5
6
7
8
9
10
11
# 移动元素
接下来我们讨论如何进行DOM移动操作
if(j > oldEnd && j <= newEnd) {
//
} else if (j > newEnd && j <= oldEnd){
//
} else {
//
for(let i = oldStart; i < oldEnd; i++) {
//
}
if(moved){
//DOM移动
}
}
2
3
4
5
6
7
8
9
10
11
12
13
在这之前我们要根据source数组计算出他的最长递增子序列.仍然用前面的例子
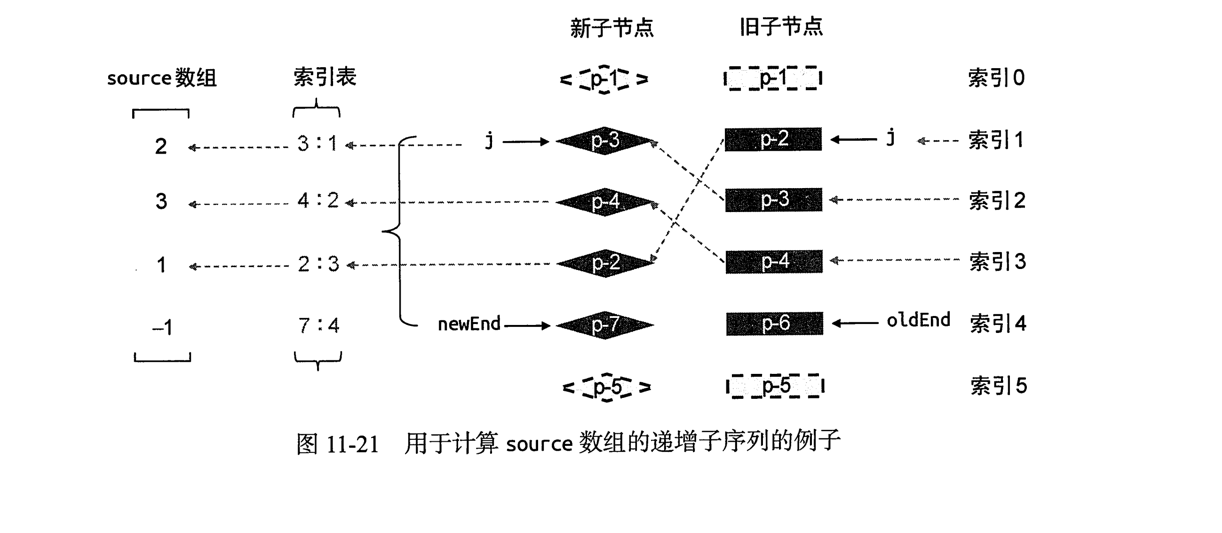我们的source数组为 [ 2 , 3 , 1, -1 ]
if(moved) {
const seq = lis(source) // [0, 1]
}
2
3
我们返回了能组成最长递增子序列的索引数组,这个数组的元素是source数组中递增子序列的索引.
我们忽略了经过预处理的节点,现在,source对应索引0的节点是p-2,1是p-3,以此类推.seq又一个非常重要的含义,按上例来说,它的含义是:
在新节点组中,重新编号后索引值为0和1的这两个节点在更新前后顺序没有发生变化
就是说明0和1的节点对应的真实DOM不需要移动.也就是说可能需要移动的节点是p-2和p-7.
为了完成节点的移动,我们需要创建两个索引值i和s
- 用i指向新子节点组中的最后一个元素
- 用s指向最长递增子序列中的最后一个元素
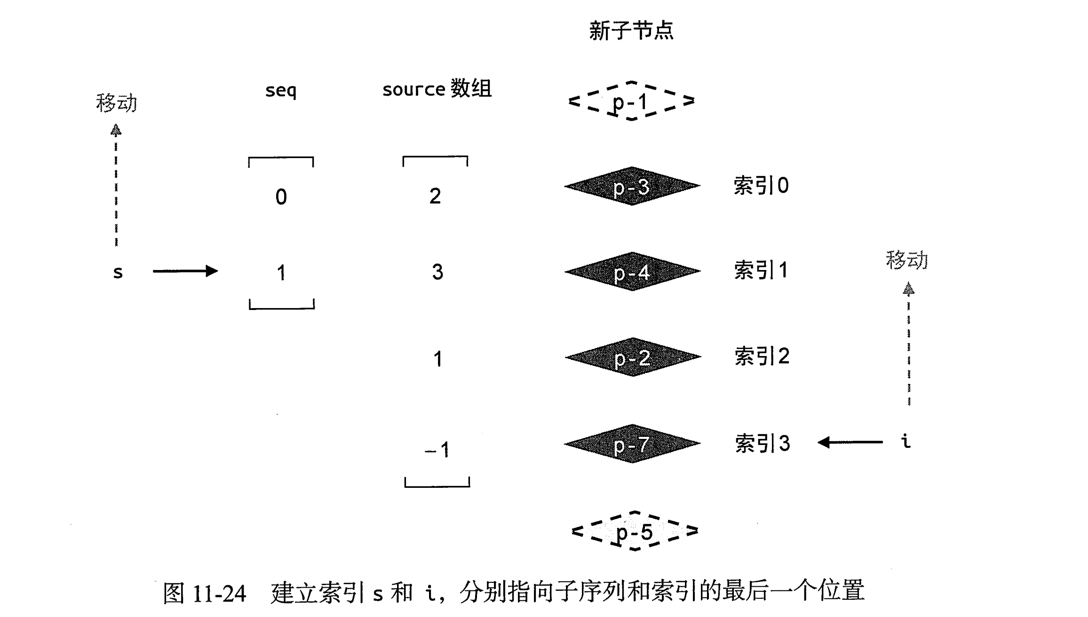
接下来,我们将开启一个for循环,让i和s按照图示方向移动.
if(moved) {
const seq = lis(source)
let s = seq.length - 1
let i = count - 1
for(i; i >= 0; i--) {
if(i !== seq[s]) {
// 如果节点索引值i不等于seq[s]的值,说明需要移动
} else {
// 当前节点索引值i等于seq[s]的值,说明不需要移动
s--
}
}
}
2
3
4
5
6
7
8
9
10
11
12
13
接下来我们按照上述思路执行更新.初始时索引i指向p-7,由于节点数组中相同位置的元素位置为 -1,所以我们一个将p-7作为全新的节点进行挂载
if(moved) {
const seq = lis(source)
let s = seq.length - 1
let i = count - 1
for(i; i >= 0; i--) {
if(source[i] === -1) {
//说明该节点是全新的节点
//该节点在新children中真实的位置索引
const pos = i + newStart
const nextPos = pos + 1
//锚点
const anchor = nextPos < newChildren.length ? newChildren[nextPos].el : null
//挂载
patch(null, newChildren[pos], container, anchor)
}
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
新节点穿件完毕后,for循环执行一次,索引i向上移动一步,指向了节点 p-2
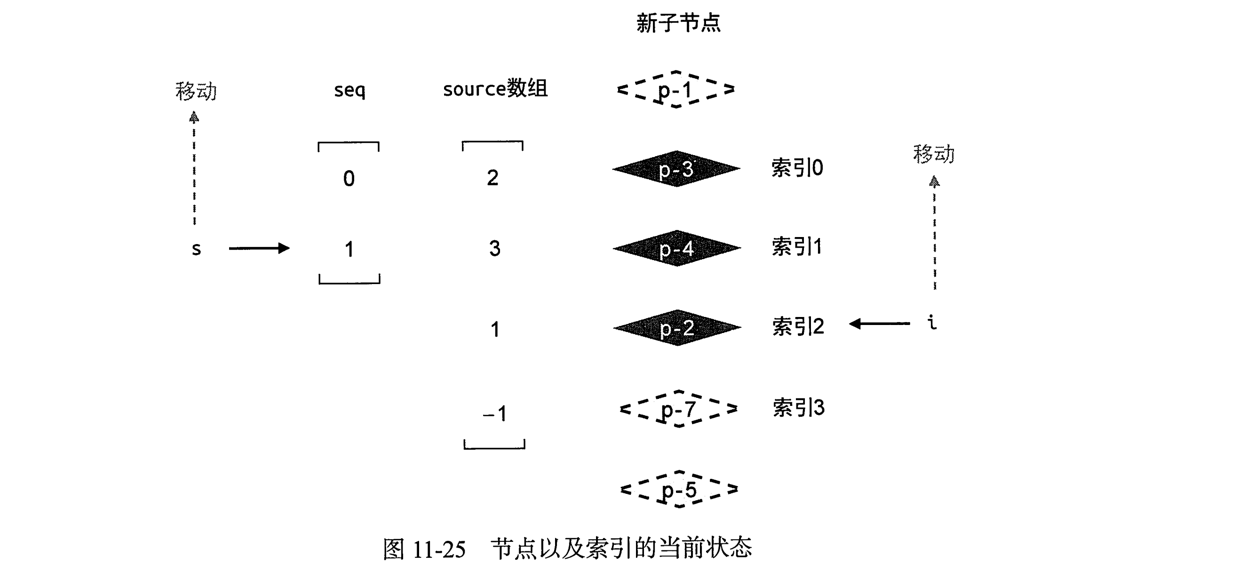这次会进入 i!==seq[s] 的分支,节点 p-2 所对应的真实DOM需要移动
if(moved) {
const seq = lis(source)
let s = seq.length - 1
let i = count - 1
for(i; i >= 0; i--) {
if(source[i] === -1) {
//
} else if(i !== seq[s]) {
// 该节点在新子节点组中的真实索引
const pos = i + newStart
const newNode = newChildren[pos]
const nextPos = pos + 1
const anchor = nextPos < newChildren.length ? newChildren[nextPos].el : null
//移动
insert(newNode.el, container, anchor)
} else {
s--
}
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
紧接着又是下一轮的循环,很明显,下两次循环都会命中 else 分支,两次for循环结束后,循环停止,更新完成!
可以自行查阅最长递增子序列的实现代码
以上就是快速diff算法中的所有内容, 图片来自《Vue的设计与实现》
写于西13